While writing a parser for Gom, I was stuck for a long time writing the parsing method for expressions. Expressions form a fundamental unit of statements in many programming languages which can often be broken down into expressions and sub-expressions. There are multiple ways to interpret a line into a tree of expressions, hence the confusion.
Consider the following line, which is a valid expression in several languages:
a + 3 * math.sum(1, 2)
It is a combination of an addition, a multiplication, a property access and a function call expressions. The way this expression will be parsed depends how your parser has been implemented but ideally, as a programmer, you'd want it to be parsed and interpreted as:
a + (3 * math.sum(1, 2))
- The
sumproperty ofmathis accessed. - It is called with 1 and 2 as arguments.
- Then the multiplication is processed with 3 and the result of
math.sum()call as operands. - Lastly, the result of multiplication is added to 3.
Essentially, when this expression is executed, you'd want the order of execution to be:
Access -> Call -> Multiplication -> Addition
This preferred order is called precedence. You'd also have other operators in this list e.g. comparison and exponential. Arithmetic precedence comes from the BODMAS (brackets of division multiplication addition subtraction) rule and comparison is of lower precedence that arithmetic. Access and call are higher precedence and terminals (e.g. number and string literals, identifiers) and bracketed expressions are of the highest precedence.
If I had to list down expressions in Gom, here's how they'd range in terms of precedence. Smaller number is higher precedence.
| Precedence | Expression |
|---|---|
| 0 | Bracketed expressions, number and string literals, identifiers, true, false |
| 1 | Access (.), call (a()) |
| 2 | Multiplication (*), division (/) |
| 3 | Addition (+), subtraction (-) |
| 4 | Exponentials (a^b) |
| 5 | Comparison ("<", ">", "<=", ">=", "==") |
| 6 | Assignment (=) |
Parsing #
Gom's parser is a hand-written recursive-descent parser. This type of parser defines parsing methods for each rule type and creates nodes that form the abstract-syntax tree. The logic for parsing comes from the language grammar. Let's consider an example of a multiplication or division expression which, in Gom, can have multiple operands each of which can be an expression. A naive approach to writing expression grammar would result in the following rule:
expr = expr ("*" | "/") expr
| (* ... other expr rules *)
| term; (* term is a terminal token, e.g. number literal *)The first problem with this grammar is that it's left-recursive, meaning the rule expands recursively on the left infinitely. This is a problem with the type of parser Gom has since it processes the program text from left to right. When trying to parse an expression, e.g. a * 2, the parser will be stuck in an infinite recursion as it will first try to parse an expression before checking an operator. To correct this, we'd have to re-write the grammar:
expr = expr ("*" | "/") expr
| term;
(* Remove left recursion by making the first value a terminal *)
expr = term expr_tail?;
expr_tail = ("*" | "/") expr;Gom's grammar can be considered to be LL(1) as tokens are processed Left to right and the Leftmost derivation is picked. The (1) denotes the lookahead size, i.e. Gom's parser can determine which rule to pick by looking ahead at most 1 token. The grammar is corrected for left recursion and also denotes the precedence order.
Precedence #
The grammar below denotes equal precedence for all operators, which is undesirable in a programming language.
expr = expr ("*" | "/") expr
| expr ("+" | "-") expr
| expr COMPARISON expr (* COMPARISON = ">=" | "<=" | "<" ... *)
| term;The solution to this is rather interesting. To denote the correct precedence while parsing, the parser should ensure that the expressions having a higher precedence are placed closer to the leaves of the abstract-syntax tree. Expressions closer to the leaves will be interpreted first and hence the precedence will be respected. We re-structure the grammar as follows:
expr = comparison;
comparison = sum (COMPARISON sum)?;
sum = quot (("+" | "-") quot)?;
quot = term (("/" | "*") term)?;
term = number | string | identifer;Let's take an example: 1 + 2 * 4 > 5. The result decision flow and the AST looks like this:
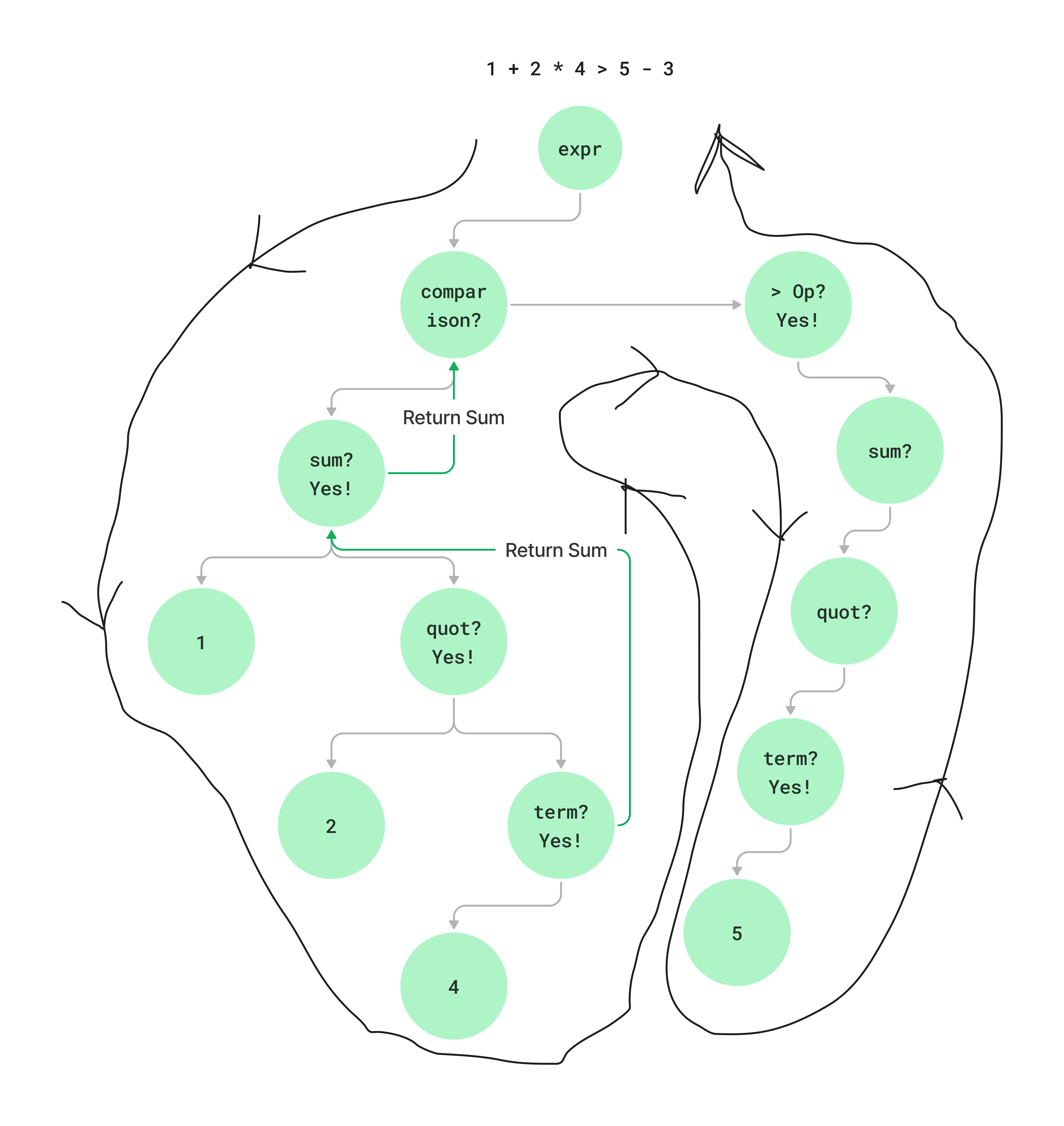
The parser should respect the precedence and implement the methods for each expression type such that high precedence types are deep into the AST. You can check Gom's parser method parseExpression() here.